Understanding Serenity, Part 2: Casper

Special thanks to Vlad Zamfir for introducing the idea of by-block consensus and convincing me of its merits, alongside many of the other core ideas of Casper, and to Vlad Zamfir and Greg Meredith for their continued work on the protocol

In the last post in this series, we discussed one of the two flagship feature sets of Serenity: a heightened degree of abstraction that greatly increases the flexibility of the platform and takes a large step in moving Ethereum from “Bitcoin plus Turing-complete” to “general-purpose decentralized computation”. Now, let us turn our attention to the other flagship feature, and the one for which the Serenity milestone was originally created: the Casper proof of stake algorithm.

Consensus By Bet

The keystone mechanism of Casper is the introduction of a fundamentally new philosophy in the field of public economic consensus: the concept of consensus-by-bet. The core idea of consensus-by-bet is simple: the protocol offers opportunities for validators to bet against the protocol on which blocks are going to be finalized. A bet on some block X in this context is a transaction which, by protocol rules, gives the validator a reward of Y coins (which are simply printed to give to the validator out of thin air, hence “against the protocol”) in all universes in which block X was processed but which gives the validator a penalty of Z coins (which are destroyed) in all universes in which block X was not processed.

The validator will wish to make such a bet only if they believe block X is likely enough to be processed in the universe that people care about that the tradeoff is worth it. And then, here’s the economically recursive fun part: the universe that people care about, ie. the state that users’ clients show when users want to know their account balance, the status of their contracts, etc, is itself derived by looking at which blocks people bet on the most. Hence, each validator’s incentive is to bet in the way that they expect others to bet in the future, driving the process toward convergence.

A helpful analogy here is to look at proof of work consensus – a protocol which seems highly unique when viewed by itself, but which can in fact be perfectly modeled as a very specific subset of consensus-by-bet. The argument is as follows. When you are mining on top of a block, you are expending electricity costs E per second in exchange for receiving a chance p per second of generating a block and receiving R coins in all forks containing your block, and zero rewards in all other chains:

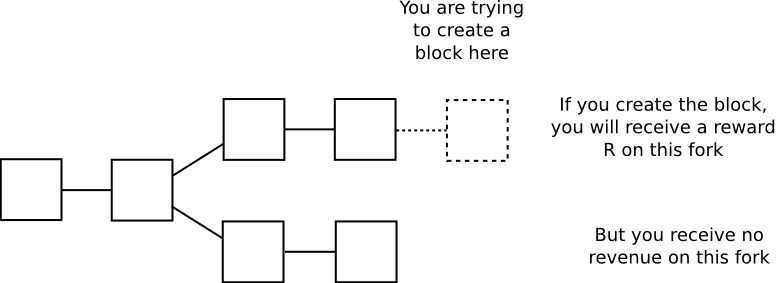
Hence, every second, you receive an expected gain of p*R-E on the chain you are mining on, and take a loss of E on all other chains; this can be interpreted as taking a bet at E:p*R-E odds that the chain you are mining on will “win”; for example, if p is 1 in 1 million, R is 25 BTC ~= $10000 USD and E is $0.007, then your gains per second on the winning chain are 0.000001 * 10000 – 0.007 = 0.003, your losses on the losing chain are the electricity cost of 0.007, and so you are betting at 7:3 odds (or 70% probability) that the chain you are mining on will win. Note that proof of work satisfies the requirement of being economically “recursive” in the way described above: users’ clients will calculate their balances by processing the chain that has the most proof of work (ie. bets) behind it.

Consensus-by-bet can be seen as a framework that encompasses this way of looking at proof of work, and yet also can be adapted to provide an economic game to incentivize convergence for many other classes of consensus protocols. Traditional Byzantine-fault-tolerant consensus protocols, for example, tend to have a concept of “pre-votes” and “pre-commits” before the final “commit” to a particular result; in a consensus-by-bet model, one can make each stage be a bet, so that participants in the later stages will have greater assurance that participants in the earlier stages “really mean it”.

It can also be used to incentivize correct behavior in out-of-band human consensus, if that is needed to overcome extreme circumstances such as a 51% attack. If someone buys up half the coins on a proof-of-stake chains, and attacks it, then the community simply needs to coordinate on a patch where clients ignore the attacker’s fork, and the attacker and anyone who plays along with the attacker automatically loses all of their coins. A very ambitious goal would be to generate these forking decisions automatically by online nodes – if done successfully, this would also subsume into the consensus-by-bet framework the underappreciated but important result from traditional fault tolerance research that, under strong synchrony assumptions, even if almost all nodes are trying to attack the system the remaining nodes can still come to consensus.

In the context of consensus-by-bet, different consensus protocols differ in only one way: who is allowed to bet, at what odds and how much? In proof of work, there is only one kind of bet offered: the ability to bet on the chain containing one’s own block at odds E:p*R-E. In generalized consensus-by-bet, we can use a mechanism known as a scoring rule to essentially offer an infinite number of betting opportunities: one infinitesimally small bet at 1:1, one infinitesimally small bet at 1.000001:1, one infinitesimally small bet at 1.000002:1, and so forth.

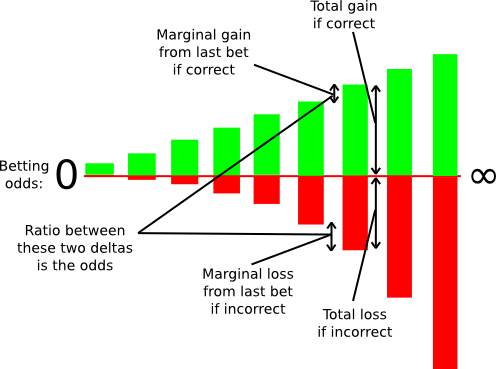
A scoring rule as an infinite number of bets.

One can still decide exactly how large these infinitesimal marginal bets are at each probability level, but in general this technique allows us to elicit a very precise reading of the probability with which some validator thinks some block is likely to be confirmed; if a validator thinks that a block will be confirmed with probability 90%, then they will accept all of the bets below 9:1 odds and none of the bets above 9:1 odds, and seeing this the protocol will be able to infer this “opinion” that the chance the block will be confirmed is 90% with exactness. In fact, the revelation principle tells us that we may as well ask the validators to supply a signed message containing their “opinion” on the probability that the block will be confirmed directly, and let the protocol calculate the bets on the validator’s behalf.

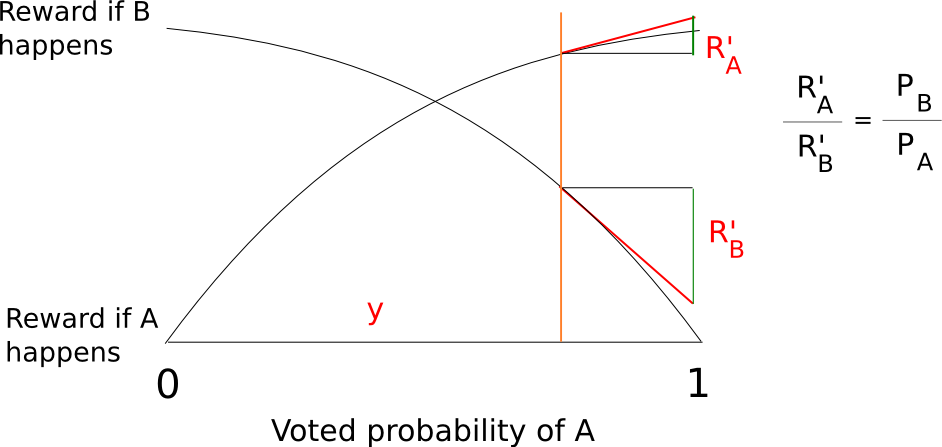
Thanks to the wonders of calculus, we can actually come up with fairly simple functions to compute a total reward and penalty at each probability level that are mathematically equivalent to summing an infinite set of bets at all probability levels below the validator’s stated confidence. A fairly simple example is s(p) = p/(1-p) and f(p) = (p/(1-p))^2/2 where s computes your reward if the event you are betting on takes place and f computes your penalty if it does not.

A key advantage of the generalized approach to consensus-by-bet is this. In proof of work, the amount of “economic weight” behind a given block increases only linearly with time: if a block has six confirmations, then reverting it only costs miners (in equilibrium) roughly six times the block reward, and if a block has six hundred confirmations then reverting it costs six hundred times the block reward. In generalized consensus-by-bet, the amount of economic weight that validators throw behind a block could increase exponentially: if most of the other validators are willing to bet at 10:1, you might be comfortable sticking your neck out at 20:1, and once almost everyone bets 20:1 you might go for 40:1 or even higher. Hence, a block may well reach a level of “de-facto complete finality”, where validators’ entire deposits are at stake backing that block, in as little as a few minutes, depending on how brave the validators are (and how much the protocol incentivizes them to be).

Blocks, Chains and Consensus as Tug of War

Another unique component of the way that Casper does things is that rather than consensus being by-chain as is the case with current proof of work protocols, consensus is by-block: the consensus process comes to a decision on the status of the block at each height independently of every other height. This mechanism does introduce some inefficiencies – particularly, a bet must register the validator’s opinion on the block at every height rather than just the head of the chain – but it proves to be much simpler to implement strategies for consensus-by-bet in this model, and it also has the advantage that it is much more friendly to high blockchain speed: theoretically, one can even have a block time that is faster than network propagation with this model, as blocks can be produced independently of each other, though with the obvious proviso that block finalization will still take a while longer.

In by-chain consensus, one can view the consensus process as being a kind of tug-of-war between negative infinity and positive infinity at each fork, where the “status” at the fork represents the number of blocks in the longest chain on the right side minus the number of blocks on the left side:

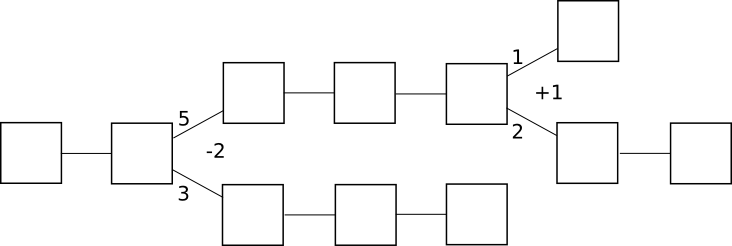
Clients trying to determine the “correct chain” simply move forward starting from the genesis block, and at each fork go left if the status is negative and right if the status is positive. The economic incentives here are also clear: once the status goes positive, there is a strong economic pressure for it to converge to positive infinity, albeit very slowly. If the status goes negative, there is a strong economic pressure for it to converge to negative infinity.

Incidentally, note that under this framework the core idea behind the GHOST scoring rule becomes a natural generalization – instead of just counting the length of the longest chain toward the status, count every block on each side of the fork:

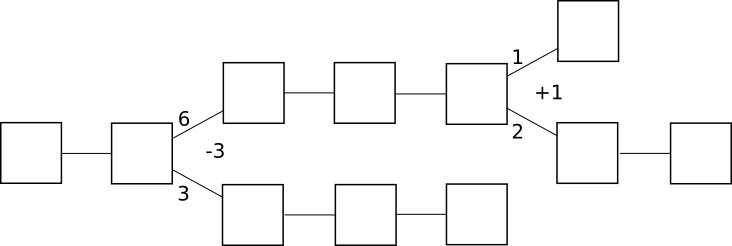
In by-block consensus, there is once again the tug of war, though this time the “status” is simply an arbitrary number that can be increased or decreased by certain actions connected to the protocol; at every block height, clients process the block if the status is positive and do not process the block if the status is negative. Note that even though proof of work is currently by-chain, it doesn’t have to be: one can easily imagine a protocol where instead of providing a parent block, a block with a valid proof of work solution must provide a +1 or -1 vote on every block height in its history; +1 votes would be rewarded only if the block that was voted on does get processed, and -1 votes would be rewarded only if the block that was voted on does not get processed:

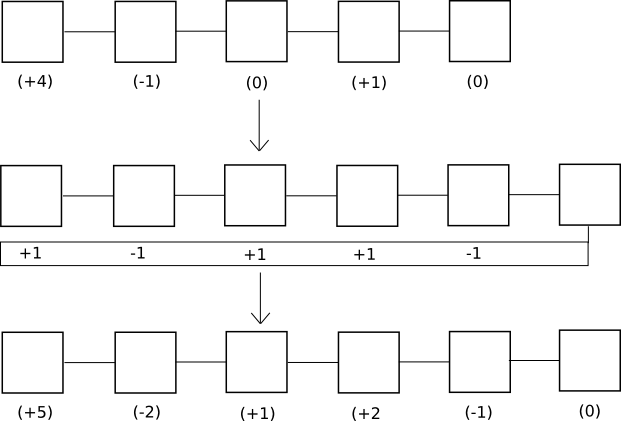
Of course, in proof of work such a design would not work well for one simple reason: if you have to vote on absolutely every previous height, then the amount of voting that needs to be done will increase quadratically with time and fairly quickly grind the system to a halt. With consensus-by-bet, however, because the tug of war can converge to complete finality exponentially, the voting overhead is much more tolerable.

One counterintuitive consequence of this mechanism is the fact that a block can remain unconfirmed even when blocks after that block are completely finalized. This may seem like a large hit in efficiency, as if there is one block whose status is flip-flopping with ten blocks on top of it then each flip would entail recalculating state transitions for an entire ten blocks, but note that in a by-chain model the exact same thing can happen between chains as well, and the by-block version actually provides users with more information: if their transaction was confirmed and finalized in block 20101, and they know that regardless of the contents of block 20100 that transaction will have a certain result, then the result that they care about is finalized even though parts of the history before the result are not. By-chain consensus algorithms can never provide this property.

So how does Casper work anyway?

In any security-deposit-based proof of stake protocol, there is a current set of bonded validators, which is kept track of as part of the state; in order to make a bet or take one of a number of critical actions in the protocol, you must be in the set so that you can be punished if you misbehave. Joining the set of bonded validators and leaving the set of bonded validators are both special transaction types, and critical actions in the protocol such as bets are also transaction types; bets may be transmitted as independent objects through the network, but they can also be included into blocks.

In keeping with Serenity’s spirit of abstraction, all of this is implemented via a Casper contract, which has functions for making bets, joining, withdrawing, and accessing consensus information, and so one can submit bets and take other actions simply by calling the Casper contract with the desired data. The state of the Casper contract looks as follows:

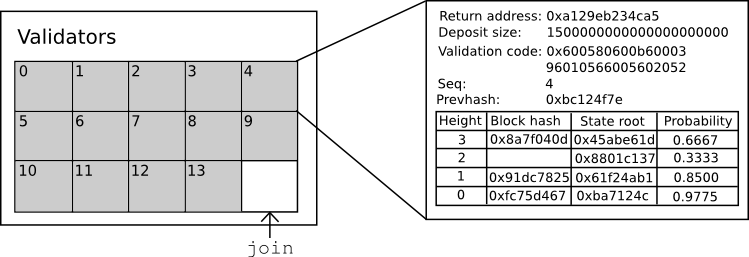
The contract keeps track of the current set of validators, and for each validator it keeps track of six primary things:

• The return address for the validator’s deposit
• The current size of the validator’s deposit (note that the bets that the validator makes will increase or decrease this value)
• The validator’s validation code
• The sequence number of the most recent bet
• The hash of the most recent bet
• The validator’s opinion table

The concept of “validation code” is another abstraction feature in Serenity; whereas other proof of stake protocols require validators to use one specific signature verification algorithm, the Casper implementation in Serenity allows validators to specify a piece of code that accepts a hash and a signature and returns 0 or 1, and before accepting a bet checks the hash of the bet against its signature. The default validation code is an ECDSA verifier, but one can also experiment with other verifiers: multisig, threshold signatures (potentially useful for creating decentralized stake pools!), Lamport signatures, etc.

Every bet must contain a sequence number one higher than the previous bet, and every bet must contain a hash of the previous bet; hence, one can view the series of bets made by a validator as being a kind of “private blockchain”; viewed in that context, the validator’s opinion is essentially the state of that chain. An opinion is a table that describes:

• What the validator thinks the most likely state root is at any given block height
• What the validator thinks the most likely block hash is at any given block height (or zero if no block hash is present)
• How likely the block with that hash is to be finalized

A bet is an object that looks like this:

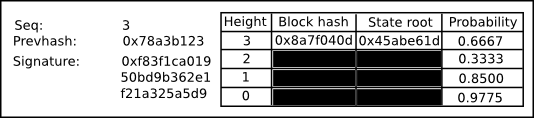
The key information is the following:

• The sequence number of the bet
• The hash of the previous bet
• A signature
• A list of updates to the opinion

The function in the Casper contract that processes a bet has three parts to it. First, it validates the sequence number, previous hash and signature of a bet. Next, it updates the opinion table with any new information supplied by the bet. A bet should generally update a few very recent probabilities, block hashes and state roots, so most of the table will generally be unchanged. Finally, it applies the scoring rule to the opinion: if the opinion says that you believe that a given block has a 99% chance of finalization, and if, in the particular universe that this particular contract is running in, the block was finalized, then you might get 99 points; otherwise you might lose 4900 points.

Note that, because the process of running this function inside the Casper contract takes place as part of the state transition function, this process is fully aware of what every previous block and state root is at least within the context of its own universe; even if, from the point of view of the outside world, the validators proposing and voting on block 20125 have no idea whether or not block 20123 will be finalized, when the validators come around to processing that block they will be – or, perhaps, they might process both universes and only later decide to stick with one. In order to prevent validators from providing different bets to different universes, we have a simple slashing condition: if you make two bets with the same sequence number, or even if you make a bet that you cannot get the Casper contract to process, you lose your entire deposit.

Withdrawing from the validator pool takes two steps. First, one must submit a bet whose maximum height is -1; this automatically ends the chain of bets and starts a four-month countdown timer (20 blocks / 100 seconds on the testnet) before the bettor can recover their funds by calling a third method, withdraw. Withdrawing can be done by anyone, and sends funds back to the same address that sent the original join transaction.

Block proposition

A block contains (i) a number representing the block height, (ii) the proposer address, (iii) a transaction root hash and (iv) a signature. For a block to be valid, the proposer address must be the same as the validator that is scheduled to generate a block for the given height, and the signature must validate when run against the validator’s own validation code. The time to submit a block at height N is determined by T = G + N * 5 where G is the genesis timestamp; hence, a block should ordinarily appear every five seconds.

An NXT-style random number generator is used to determine who can generate a block at each height; essentially, this involves taking missing block proposers as a source of entropy. The reasoning behind this is that even though this entropy is manipulable, manipulation comes at a high cost: one must sacrifice one’s right to create a block and collect transaction fees in order to manipulate it. If it is deemed absolutely necessary, the cost of manipulation can be increased several orders of magnitude further by replacing the NXT-style RNG with a RANDAO-like protocol.

The Validator Strategy

So how does a validator operate under the Casper protocol? Validators have two primary categories of activity: making blocks and making bets. Making blocks is a process that takes place independently from everything else: validators gather transactions, and when it comes time for them to make a block, they produce one, sign it and send it out to the network. The process for making bets is more complicated. The current default validator strategy in Casper is one that is designed to mimic aspects of traditional Byzantine-fault-tolerant consensus: look at how other validators are betting, take the 33rd percentile, and move a step toward 0 or 1 from there.

To accomplish this, each validator collects and tries to stay as up-to-date as possible on the bets being made by all other validators, and keeps track of the current opinion of each one. If there are no or few opinions on a particular block height from other validators, then it follows an initial algorithm that looks roughly as follows:

• If the block is not yet present, but the current time is still very close to the time that the block should have been published, bet 0.5
• If the block is not yet present, but a long time has already passed since the block should have been published, bet 0.3
• If the block is present, and it arrived on time, bet 0.7
• If the block is present, but it arrived either far too early or far too late, bet 0.3

Some randomness is added in order to help prevent “stuck” scenarios, but the basic principle remains the same.

If there are already many opinions on a particular block height from other validators, then we take the following strategy:

• Let L be the value such that two thirds of validators are betting higher than L. Let M be the median (ie. the value such that half of validators are betting higher than M). Let H be the value such that two thirds of validators are betting lower than H.
• Let e(x) be a function that makes x more “extreme”, ie. pushes the value away from 0.5 and toward 1. A simple example is the piecewise function e(x) = 0.5 + x / 2 if x > 0.5 else x / 2.
• If L > 0.8, bet e(L)
• If H < 0.2, bet e(H)
• Otherwise, bet e(M), though limit the result to be within the range [0.15, 0.85] so that less than 67% of validators can’t force another validator to move their bets too far

Validators are free to choose their own level of risk aversion within the context of this strategy by choosing the shape of e. A function where f(e) = 0.99999 for e > 0.8 could work (and would in fact likely provide the same behavior as Tendermint) but it creates somewhat higher risks and allows hostile validators making up a large portion of the bonded validator set to trick these validators into losing their entire deposit at a low cost (the attack strategy would be to bet 0.9, trick the other validators into betting 0.99999, and then jump back to betting 0.1 and force the system to converge to zero). On the other hand, a function that converges very slowly will incur higher inefficiencies when the system is not under attack, as finality will come more slowly and validators will need to keep betting on each height longer.

Now, how does a client determine what the current state is? Essentially, the process is as follows. It starts off by downloading all blocks and all bets. It then uses the same algorithm as above to construct its own opinion, but it does not publish it. Instead, it simply looks at each height sequentially, processing a block if its probability is greater than 0.5 and skipping it otherwise; the state after processing all of these blocks is shown as the “current state” of the blockchain. The client can also provide a subjective notion of “finality”: when the opinion at every height up to some k is either above 99.999% or below 0.001%, then the client considers the first k blocks finalized.

Further Research

There is still quite a bit of research to do for Casper and generalized consensus-by-bet. Particular points include:

• Coming up with results to show that the system economically incentivizes convergence, even in the presence of some quantity of Byzantine validators
• Determining optimal validator strategies
• Making sure that the mechanism for including the bets in blocks is not exploitable
• Increasing efficiency. Currently, the POC1 simulation can handle ~16 validators running at the same time (up from ~13 a week ago), though ideally we should push this up as much as possible (note that the number of validators the system can handle on a live network should be roughly the square of the performance of the POC, as the POC runs all nodes on the same machine).

The next article in this series will deal with efforts to add a scaffolding for scalability into Serenity, and will likely be released around the same time as POC2.